Position calculation advanced

Before providing a more mathematical description of position calculation, the introductory material on this topics is reviewed. To describe the basic concept of how a GPS receiver works, the errors are at first ignored. Using messages received from four satellites, the GPS receiver is able to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as where the subscript i denotes which satellite and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received , the GPS receiver can compute the indicated transit time, 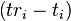. of the message. Assuming the message traveled at the speed of light, c, the distance traveled, 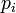can be computed as . Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres if they intersect in more than one point intersect in a circle. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below depicting this which hopefully will aid the reader in visualizing this intersection.

The article, trilateration, shows mathematically how the equation for a circle is determined. A circle and sphere surface in most cases of practical interest intersect at two points, although it is conceivable that they could intersect in 0, 1 or infinite points. Another figure, Surface of Sphere Intersecting a Circle (not disk) at Two Points, is shown below to aid in visualizing this intersection. Again trilateration clearly show this mathematically. The correct position of the GPS receiver is the one that is closest to the fourth sphere. This paragraph has described the basic concept of GPS while ignoring errors. The next problem is how to process the messages when errors are present.

Let denote the clock error or bias, the amount by which the receiver's clock is slow. The GPS receiver has four unknowns, the three components of GPS receiver position and the clock bias . The equation of the sphere surfaces are given by

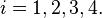, Another useful form of these equations is in terms of the pseudoranges, which are simply the ranges approximated based on GPS receiver clock's indicated (i.e. uncorrected) time so that . Then the equations becomes:

. Two of the most important methods of computing GPS receiver position and clock bias are (1) trilateration followed by one dimensional numerical root finding and (2) multidimensional Newton-Raphson calculations. These two methods along with their advantages are discussed.

• The receiver can solve by trilateration followed by one dimensional numerical root finding^[. This method involves using Trilateration to determine the intersection of the surfaces of three spheres. It is clearly shown in trilateration that the surfaces of three spheres intersect in 0, 1, or 2 points. In the usual case of two intersections, the solution which is nearest the surface of the sphere corresponding to the fourth satellite is chosen. The surface of the earth can also sometimes be used instead, especially in the case of civilian GPS receivers since it is illegal in the United States to track vehicles of more than 60,000 feet in altitude. The bias, is then computed based on the distance from the solution to the surface of the sphere corresponding to the fourth satellite. Using an updated received time based on this bias, new spheres are computed and the process is repeated. One advantage of this method is that it involves one dimensional as opposed to multidimensional numerical root finding.

• The receiver can utilize multidimensional Newton-Raphson calculations. Linearize around an approximate solution, say from iteration k, then solve four linear equations derived from the quadratic equations above to obtain . The radii are large and so the sphere surfaces are close to flat.^[28][29] This near flatness may cause the iterative procedure to converge rapidly in the case where is near the correct value and the primary change is in the values of , since in this case the problem is merely to find the intersection of nearly flat surfaces and thus close to a linear problem. However when is changing significantly, this near flatness does not appear to be advantageous in producing rapid convergence, since in this case these near flat surfaces will be moving as the spheres expand and contract. This possible fast convergence is an advantage of this method. Also it has been claimed that this method is the "typical" method used by GPS receivers. A disadvantage of this method is that according to , "There are no good general methods for solving systems of more than one nonlinear equations." For a more detailed description of the mathematics see Multidimensional Newton Raphson.

• Other methods include:

1. Solving for the intersection of the expanding signals form light cones in 4-space cones
2. Solving for the intersection of hyperboloids determined by the time difference of signals received from satellites utilizing multilateration,
3. Solving the equations in accordance with.

• More than four satellites should be used, if available. This results in an over-determined system of equations with no unique solution, which must be solved by least-squares or a similar technique. If all visible satellites are used, the results are always at least as good as using the four best, and usually better. Also the errors in results can be estimated through the residuals. With each combination of four or more satellites, a geometric dilution of precision (GDOP) vector can be calculated, based on the relative sky positions of the satellites used. As more satellites are picked up, pseudoranges from more combinations of four satellites can be processed to add more estimates to the location and clock offset. The receiver then determines which combinations to use and how to calculate the estimated position by determining the weighted average of these positions and clock offsets. After the final location and time are calculated, the location is expressed in a specific coordinate system such as latitude and longitude, using the WGS 84 geodetic datum or a local system specific to a country.

Finally, results from other positioning systems such as GLONASS or the upcoming Galileo can be used in the fit, or used to double check the result. (By design, these systems use the same bands, so much of the receiver circuitry can be shared, though the decoding is different.)

C/A code: Demodulation and decoding

Since all of the satellite signals are modulated onto the same L1 carrier frequency, there is a need to separate the signals after demodulation. This is done by assigning each satellite a unique pseudorandom sequence known as a Gold code, and the signals are decoded, after demodulation, using modulo 2 addition of the Gold codes corresponding to satellites n₁ through n_k, where k is the number of channels in the GPS receiver and n₁ through n_k are the pseudorandom numbers associated with the satellites. The result of these modulo 2 additions are the 50 bps navigation messages from satellites n₁ through n_k. The Gold codes used in GPS are a sequence of 1023 bits with a period of one millisecond. These Gold codes are highly mutually orthogonal, so that it is unlikely that one satellite signal will be misinterpreted as another. As well, the Gold codes have good auto-correlation properties.

There are 1025 different Gold codes of length 1023 bits, but only 32 are used. These Gold codes are quite often referred to as "pseudo-random noise" since they contain no data. However, this may be misleading since they are actually deterministic sequences.

If the almanac information has previously been acquired, the receiver picks which satellites to listen for by their PRN numbers. If the almanac information is not in memory, the receiver enters a search mode and cycles through the PRN numbers until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern, then measures the received time for each satellite. To do this, the receiver produces an identical C/A sequence using the same PRN number as depicted in the diagram, referenced to its local clock, starting at the same time the satellite sent it. It then computes the offset to the local clock that generates the maximum correlation. This offset is the time delay from the satellite to the receiver, as told by the receiver's clock. Since the PRN repeats every millisecond, this offset is precise but ambiguous, and the ambiguity is resolved by looking at the data bits, which are sent at 50 Hz (20 ms/bit) and aligned with the PRN code.

Next, the orbital position data, or ephemeris, from the Navigation Message is then downloaded to calculate precisely where the satellite was at the start of the message. A more-sensitive receiver will potentially acquire the ephemeris data more quickly than a less-sensitive receiver, especially in a noisy environment.

Navigation signals

Each GPS satellite continuously broadcasts a Navigation Message at 50 bit/s giving the time-of-week, GPS week number and satellite health information (all transmitted in the first part of the message), an ephemeris (transmitted in the second part of the message) and an almanac (later part of the message). The messages are sent in frames, each taking 30 seconds to transmit 1500 bits.

The first 6 seconds of every frame contains data describing the satellite clock and its relationship to GPS time. The next 12 seconds contain the ephemeris data, giving the satellite's own precise orbit. The ephemeris is updated every 2 hours and is generally valid for 4 hours, with provisions for updates every 6 hours or longer in non-nominal conditions. The time needed to acquire the ephemeris is becoming a significant element of the delay to first position fix, because, as the hardware becomes more capable, the time to lock onto the satellite signals shrinks, but the ephemeris data requires 30 seconds (worst case) before it is received, due to the low data transmission rate.

The almanac consists of coarse orbit and status information for each satellite in the constellation, an ionospheric model, and information to relate GPS derived time to Coordinated Universal Time (UTC). A new part of the almanac is received for the last 12 seconds in each 30 second frame. Each frame contains 1/25th of the almanac, so 12.5 minutes are required to receive the entire almanac from a single satellite. The almanac serves several purposes. The first is to assist in the acquisition of satellites at power-up by allowing the receiver to generate a list of visible satellites based on stored position and time, while an ephemeris from each satellite is needed to compute position fixes using that satellite. In older hardware, lack of an almanac in a new receiver would cause long delays before providing a valid position, because the search for each satellite was a slow process. Advances in hardware have made the acquisition process much faster, so not having an almanac is no longer an issue. The second purpose is for relating time derived from the GPS (called GPS time) to the international time standard of UTC. Finally, the almanac allows a single frequency receiver to correct for ionospheric error by using a global ionospheric model. The corrections are not as accurate as augmentation systems like WAAS or dual frequency receivers. However it is often better than no correction since ionospheric error is the largest error source for a single frequency GPS receiver. An important thing to note about navigation data is that each satellite transmits only its own ephemeris, but transmits an almanac for all satellites.

Each satellite transmits its navigation message with at least two distinct spread spectrum codes: the Coarse / Acquisition (C/A) code, which is freely available to the public, and the Precise (P) code, which is usually encrypted and reserved for military applications. The C/A code is a 1023 length Gold code at 1.023 million chips per second so that it repeats every millisecond. As pointed out in , a chip is essentially the same thing as a bit and chips per second is the same as bits per second. The justification for coming up with this new term, chip, is that in some cases a sequence of bits is used as a type of modulation and contains no information.

Each satellite has its own C/A code so that it can be uniquely identified and received separately from the other satellites transmitting on the same frequency. The P-code is a 10.23 megachip per second PRN code that repeats only every week. When the "anti-spoofing" mode is on, as it is in normal operation, the P code is encrypted by the Y-code to produce the P(Y) code, which can only be decrypted by units with a valid decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.

User Segment

The user's GPS receiver is the user segment (US) of the GPS. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly-stable clock (often a crystal oscillator). They may also include a display for providing location and speed information to the user. A receiver is often described by its number of channels: this signifies how many satellites it can monitor simultaneously. Originally limited to four or five, this has progressively increased over the years so that, as of 2007, receivers typically have between 12 and 20 channels.

GPS receivers may include an input for differential corrections, using the RTCM SC-104 format. This is typically in the form of a RS-232 port at 4,800 bit/s speed. Data is actually sent at a much lower rate, which limits the accuracy of the signal sent using RTCM. Receivers with internal DGPS receivers can outperform those using external RTCM data. As of 2006, even low-cost units commonly include Wide Area Augmentation System (WAAS) receivers.

Many GPS receivers can relay position data to a PC or other device using the NMEA 0183 protocol, or the newer and less widely used NMEA 2000. Although these protocols are officially defined by the NMEA, references to the these protocols have been compiled from public records, allowing open source tools like gpsd to read the protocol without violating intellectual property laws. Other proprietary protocols exist as well, such as the SiRF and MTK protocols. Receivers can interface with other devices using methods including a serial connection, USB or Bluetooth.

System segmentation and Space segment

The current GPS consists of three major segments. These are the space segment (SS), a control segment (CS), and a user segment (US).

The space segment (SS) comprises the orbiting GPS satellites, or Space Vehicles (SV) in GPS parlance. The GPS design originally called for 24 SVs, eight each in three circular orbital planes, but this was modified to six planes with four satellites each. The orbital planes are centered on the Earth, not rotating with respect to the distant stars. The six planes have approximately 55° inclination (tilt relative to Earth's equator) and are separated by 60° right ascension of the ascending node (angle along the equator from a reference point to the orbit's intersection).The orbits are arranged so that at least six satellites are always within line of sight from almost everywhere on Earth's surface.

Orbiting at an altitude of approximately 20,200 kilometers (12,600 miles or 10,900 nautical miles; orbital radius of 26,600 km (16,500 mi or 14,400 NM)), each SV makes two complete orbits each sidereal day.The ground track of each satellite therefore repeats each (sidereal) day. This was very helpful during development, since even with just four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones.

As of March 2008, there are 31 actively broadcasting satellites in the GPS constellation. The additional satellites improve the precision of GPS receiver calculations by providing redundant measurements. With the increased number of satellites, the constellation was changed to a nonuniform arrangement. Such an arrangement was shown to improve reliability and availability of the system, relative to a uniform system, when multiple satellites fail.

Some reports in 2008 indicated that the 32nd satellite was causing difficulties for some GPS receivers.

Correcting GPS clock

The method of calculating position for the case of no errors has been explained. One of the most important errors is the error in the GPS receiver clock. Because of the very large value of c, the speed of light, the estimated distances from the GPS receiver to the satellites, the pseudoranges, are very sensitive to errors in the GPS receiver clock. This seems to suggest that an extremely accurate and expensive clock is required for the GPS receiver to work. On the other hand, manufacturers would like to make an inexpensive GPS receiver which can be mass marketed. The manufacturers were thus faced with a difficult design problem. The technique that solves this problem is based on the way sphere surfaces intersect in the GPS problem.

It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let 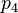denote the pseudorange of the fourth satellite. Let . Note that is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient, , provides an estimate of

(correct time) - (time indicated by the receiver's on-board clock), and the GPS receiver clock can be advanced if is positive or delayed if is negative.

Position calculation introduction

To provide an introductory description of how a GPS receiver works, errors will be ignored in this section. Using messages received from a minimum of four visible satellites, a GPS receiver is able to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as where the subscript i denotes the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received , the GPS receiver can compute the indicated transit time, . of the message. Assuming the message traveled at the speed of light, c, the distance travel led, can be computed as . Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres if they intersect in more than one point intersect in a circle. A figure, two sphere surfaces intersecting in a circle, is shown below. Two points at which the surfaces of the spheres intersect are clearly shown in the figure. The distance between these two points is the diameter of the circle of intersection. If you are not convinced of this, consider how a side view of the intersecting spheres would look. This view would look exactly the same as the figure because of the symmetry of the spheres. And in fact a view from any horizontal direction would look exactly the same. This should make it clear to the reader that the surfaces of the two spheres actually do intersect in a circle.

The article, trilateration, shows mathematically that two spheres intersecting in more than one point intersect in a circle.Surface of a sphere intersecting a circle (i.e., the edge of a disk) at two points

A circle and sphere surface in most cases of practical interest intersect at two points, although it is conceivable that they could intersect in 0 or 1 point. Another figure, Surface of Sphere Intersecting a Circle (not disk) at Two Points, is shown to aid in visualizing this intersection. Again trilateration clearly show this mathematically. The correct position of the GPS receiver is the intersection that is closest to the surface of the earth for automobiles and other near earth vehicles. The correct position of the GPS receiver is also the intersection which is closest to the surface of the sphere corresponding to the fourth satellite. (The two intersections are symmetrical with respect to the plane containing the three satellites. If the three satellites are not in the same orbital plane, the plane containing the three satellites will not be a vertical plane passing through the center of the earth. In this case one of the intersections will be closer to the earth than the other. The near-earth intersection will be the correct position for the case of a near-earth vehicle. The intersection which is farthest from earth, may be the correct position for the case of GPS systems in deep space probes or other vehicles.)

Global Positioning System

The Global Positioning System (GPS) is the only fully functional Global Navigation Satellite System (GNSS). The GPS uses a constellation of between 24 and 32 Medium Earth Orbit satellites that transmit precise microwave signals, that enable GPS receivers to determine their current location, the time, and their velocity (including direction). GPS was developed by the United States Department of Defense. Its official name is NAVSTAR-GPS. Although NAVSTAR-GPS is not an acronym, a few backronyms have been created for it.The GPS satellite constellation is managed by the United States Air Force 50th Space Wing.

Similar satellite navigation systems include the Russian GLONASS (incomplete as of 2008), the upcoming European Galileo positioning system, the proposed COMPASS navigation system of China, and IRNSS of India.

Following the shooting down of Korean Air Lines Flight 007 in 1983 after it strayed into prohibited airspace, President Ronald Reagan issued a directive making the system available free for civilian use as a common good.^[3] Since then, GPS has become a widely used aid to navigation worldwide, and a useful tool for map-making, land surveying, commerce, scientific uses, and hobbies such as geocaching. Also, the precise time reference is used in many applications including scientific study of earthquakes, and synchronization of telecommunications networks.

Computer engineering

Computer engineering deals with the design of computers and computer systems. This may involve the design of new hardware, the design of PDAs or the use of computers to control an industrial plant. Computer engineers may also work on a system's software. However, the design of complex software systems is often the domain of software engineering, which is usually considered a separate discipline. Desktop computers represent a tiny fraction of the devices a computer engineer might work on, as computer-like architectures are now found in a range of devices including video game consoles and DVD players

Instrumentation engineering

Instrumentation engineering deals with the design of devices to measure physical quantities such as pressure, flow and temperature. The design of such instrumentation requires a good understanding of physics that often extends beyond electromagnetic theory. For example, radar guns use the Doppler effect to measure the speed of oncoming vehicles. Similarly, thermocouples use the Peltier-Seebeck effect to measure the temperature difference between two points. Often instrumentation is not used by itself, but instead as the sensors of larger electrical systems. For example, a thermocouple might be used to help ensure a furnace's temperature remains constant. For this reason, instrumentation engineering is often viewed as the counterpart of control engineering.

Telecommunications engineering

Telecommunications engineering focuses on the transmission of information across a channel such as a coax cable, optical fiber or free space. Transmissions across free space require information to be encoded in a carrier wave in order to shift the information to a carrier frequency suitable for transmission, this is known as modulation. Popular analog modulation techniques include amplitude modulation and frequency modulation. The choice of modulation affects the cost and performance of a system and these two factors must be balanced carefully by the engineer.

Once the transmission characteristics of a system are determined, telecommunication engineers design the transmitters and receivers needed for such systems. These two are sometimes combined to form a two-way communication device known as a transceiver. A key consideration in the design of transmitters is their power consumption as this is closely related to their signal strength. If the signal strength of a transmitter is insufficient the signal's information will be corrupted by noise.

Signal processing

Signal processing deals with the analysis and manipulations of signals. Signals can be either analog, in which case the signal varies continuously according to the information, or digital, in which case the signal varies according to a series of discrete values representing the information. For analog signals, signal processing may involve the amplification and filtering of audio signals for audio equipment or the modulation and demodulation of signals for telecommunications. For digital signals, signal processing may involve the compression, error detection and error correction of digitally sampled signals.

Microelectronics

Microelectronics engineering deals with the design and microfabrication of very small electronic circuit components for use in an integrated circuit or sometimes for use on their own as a general electronic component. The most common microelectronic components are semiconductor transistors, although all main electronic components (resistors, capacitors, inductors) can be created at a microscopic level.

Microelectronic components are created by chemically fabricating wafers of semiconductors such as silicon (at higher frequencies, compound semiconductors like gallium arsenide and indium phosphide) to obtain the desired transport of electronic charge and control of current. The field of microelectronics involves a significant amount of chemistry and material science and requires the electronic engineer working in the field to have a very good working knowledge of the effects of quantum mechanics.

Electronic Engineering

Electronic engineering involves the design and testing of electronic circuits that use the properties of components such as resistors, capacitors, inductors, diodes and transistors to achieve a particular functionality. The tuned circuit, which allows the user of a radio to filter out all but a single station, is just one example of such a circuit. Another example (of a pneumatic signal conditioner) is shown in the adjacent photograph.

Prior to the second world war, the subject was commonly known as radio engineering and basically was restricted to aspects of communications and radar, commercial radio and early television. Later, in post war years, as consumer devices began to be developed, the field grew to include modern television, audio systems, computers and microprocessors. In the mid to late 1950s, the term radio engineering gradually gave way to the name electronic engineering.

Before the invention of the integrated circuit in 1959, electronic circuits were constructed from discrete components that could be manipulated by humans. These discrete circuits consumed much space and power and were limited in speed, although they are still common in some applications. By contrast, integrated circuits packed a large number—often millions—of tiny electrical components, mainly transistors, into a small chip around the size of a coin. This allowed for the powerful computers and other electronic devices we see today.

Control Engineering

Control engineering focuses on the modeling of a diverse range of dynamic systems and the design of controllers that will cause these systems to behave in the desired manner. To implement such controllers electrical engineers may use electrical circuits, digital signal processors, microcomputers and PLCs (Programmable Logic Controllers). Control engineering has a wide range of applications from the flight and propulsion systems of commercial airliners to the cruise control present in many modern automobiles. It also plays an important role in industrial automation.

Control engineers often utilize feedback when designing control systems. For example, in an automobile with cruise control the vehicle's speed is continuously monitored and fed back to the system which adjusts the motor's power output accordingly. Where there is regular feedback, control theory can be used to determine how the system responds to such feedback.