Correcting GPS clock

The method of calculating position for the case of no errors has been explained. One of the most important errors is the error in the GPS receiver clock. Because of the very large value of c, the speed of light, the estimated distances from the GPS receiver to the satellites, the pseudoranges, are very sensitive to errors in the GPS receiver clock. This seems to suggest that an extremely accurate and expensive clock is required for the GPS receiver to work. On the other hand, manufacturers would like to make an inexpensive GPS receiver which can be mass marketed. The manufacturers were thus faced with a difficult design problem. The technique that solves this problem is based on the way sphere surfaces intersect in the GPS problem.

It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let 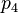denote the pseudorange of the fourth satellite. Let . Note that is the distance from the computed GPS receiver position to the surface of the sphere corresponding to the fourth satellite. Thus the quotient, , provides an estimate of

(correct time) - (time indicated by the receiver's on-board clock), and the GPS receiver clock can be advanced if is positive or delayed if is negative.