Position calculation introduction

To provide an introductory description of how a GPS receiver works, errors will be ignored in this section. Using messages received from a minimum of four visible satellites, a GPS receiver is able to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as where the subscript i denotes the satellite number and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received , the GPS receiver can compute the indicated transit time, 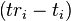. of the message. Assuming the message traveled at the speed of light, c, the distance travel led, 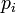can be computed as . Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres if they intersect in more than one point intersect in a circle. A figure, two sphere surfaces intersecting in a circle, is shown below. Two points at which the surfaces of the spheres intersect are clearly shown in the figure. The distance between these two points is the diameter of the circle of intersection. If you are not convinced of this, consider how a side view of the intersecting spheres would look. This view would look exactly the same as the figure because of the symmetry of the spheres. And in fact a view from any horizontal direction would look exactly the same. This should make it clear to the reader that the surfaces of the two spheres actually do intersect in a circle.

The article, trilateration, shows mathematically that two spheres intersecting in more than one point intersect in a circle.Surface of a sphere intersecting a circle (i.e., the edge of a disk) at two points

A circle and sphere surface in most cases of practical interest intersect at two points, although it is conceivable that they could intersect in 0 or 1 point. Another figure, Surface of Sphere Intersecting a Circle (not disk) at Two Points, is shown to aid in visualizing this intersection. Again trilateration clearly show this mathematically. The correct position of the GPS receiver is the intersection that is closest to the surface of the earth for automobiles and other near earth vehicles. The correct position of the GPS receiver is also the intersection which is closest to the surface of the sphere corresponding to the fourth satellite. (The two intersections are symmetrical with respect to the plane containing the three satellites. If the three satellites are not in the same orbital plane, the plane containing the three satellites will not be a vertical plane passing through the center of the earth. In this case one of the intersections will be closer to the earth than the other. The near-earth intersection will be the correct position for the case of a near-earth vehicle. The intersection which is farthest from earth, may be the correct position for the case of GPS systems in deep space probes or other vehicles.)